A Thermodynamic Foundation for the Second Law of Infodynamics

Ian Todd

doi:10.59973/ipil.308

Authors

Ian Todd Sydney Medical School, University of Sydney, Sydney, NSW, Australia

DOI:

https://doi.org/10.59973/ipil.308

Keywords:

second law of infodynamics, Landauer principle, symmetry, dimensionality, stochastic thermodynamics, Information Entropy

Abstract

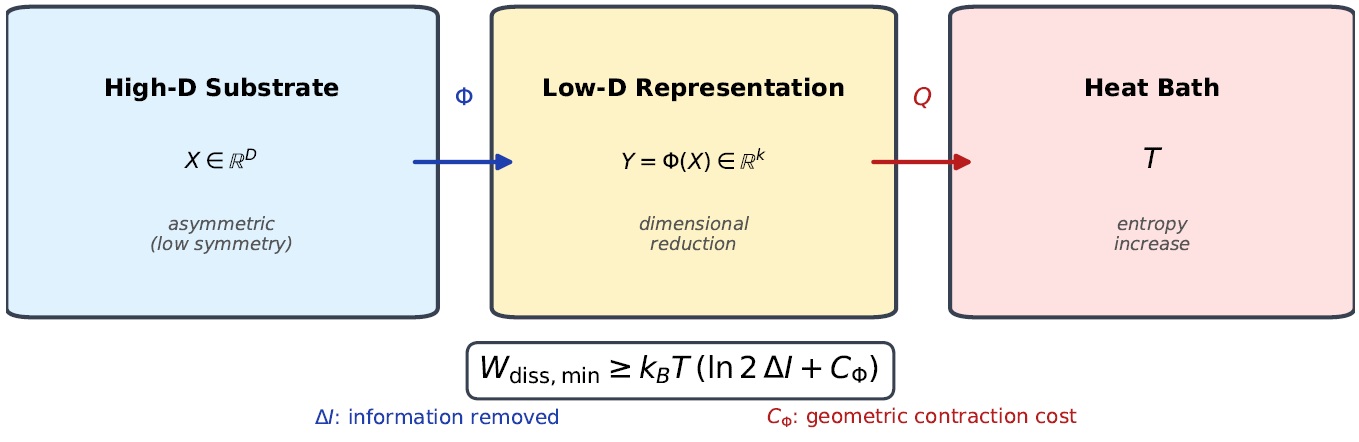
Vopson and Lepadatu’s “second law of infodynamics” proposes that the information entropy of physical systems decreases over time, with high-symmetry states representing minimum information entropy. We interpret this information entropy as structure-information: the relative entropy Istruct = DKL(p∥piso) measuring a distribution’s departure from isotropic equilibrium. This paper provides a thermodynamic mechanism for the decrease of structure-information. We derive a bound showing that maintaining a low-dimensional (asymmetric) state requires continuous work input with two components: an informational term and a geometric contraction term governed by the Jacobian of the projection map. Without this work, systems relax toward high-symmetry equilibrium where Istruct → 0. The second law of infodynamics thus emerges from a
thermodynamic asymmetry: symmetric states require no work to maintain, while asymmetric states are thermodynamically costly. This does not contradict the second law of thermodynamics—thermodynamic entropy increases in the bath precisely because structure-information is being dissipated.

References

R. Landauer, Irreversibility and heat generation in the computing process, IBM Journal of Research and Development 5(3), 183-191 (1961)

C.H. Bennett, The thermodynamics of computation-a review, International Journal of Theoretical Physics 21(12), 905-940 (1982)

A. B´erut, A. Arakelyan, A. Petrosyan, S. Ciliberto, R. Dillenschneider, E. Lutz, Experimental verification of Landauer’s principle

linking information and thermodynamics, Nature 483(7388), 187-189 (2012)

J.M.R. Parrondo, J.M. Horowitz, T. Sagawa, Thermodynamics of information, Nature Physics 11, 131-139 (2015)

U. Seifert, Stochastic thermodynamics, fluctuation theorems and molecular machines, Reports on Progress in Physics 75(12), 126001 (2012)

M.M. Vopson, S. Lepadatu, Second law of information dynamics, AIP Advances 12(7), 075310 (2022)

M.M. Vopson, The second law of infodynamics and its implications for the simulated universe hypothesis, AIP Advances 13(10), 105308 (2023)

M.M. Vopson, The mass-energy-information equivalence principle, AIP Advances 9(9), 095206 (2019)

Y. Oono, M. Paniconi, Steady state thermodynamics, Progress of Theoretical Physics Supplement 130, 29-44 (1998)

E. Noether, Invariante Variationsprobleme, Nachrichten von der Gesellschaft der Wissenschaften zu G ¨ottingen, Mathematisch-Physikalische Klasse, 235-257 (1918)

H. Weyl, Symmetry, Princeton University Press (1952)

L.D. Landau, On the theory of phase transitions, Zhurnal Eksperimental’noi i Teoreticheskoi Fiziki 7, 19-32 (1937)

P.W. Anderson, More is different, Science 177(4047), 393-396 (1972)

I. Todd, The limits of falsifiability: Dimensionality, measurement thresholds, and the sub-Landauer domain in biological systems, BioSystems, 105608 (2025)

I. Todd, Timing inaccessibility and the projection bound: Resolving Maxwell’s demon for continuous biological substrates, BioSystems, 105632 (2025)

J.P. Cunningham, B.M. Yu, Dimensionality reduction for large-scale neural recordings, Nature Neuroscience 17(11), 1500-1509 (2014)

J.A. Gallego, M.G. Perich, L.E. Miller, S.A. Solla, Neural manifolds for the control of movement, Neuron 94(5), 978-984 (2017)