Extending the Standard Model through Generation Number Reinterpretation

Abstract

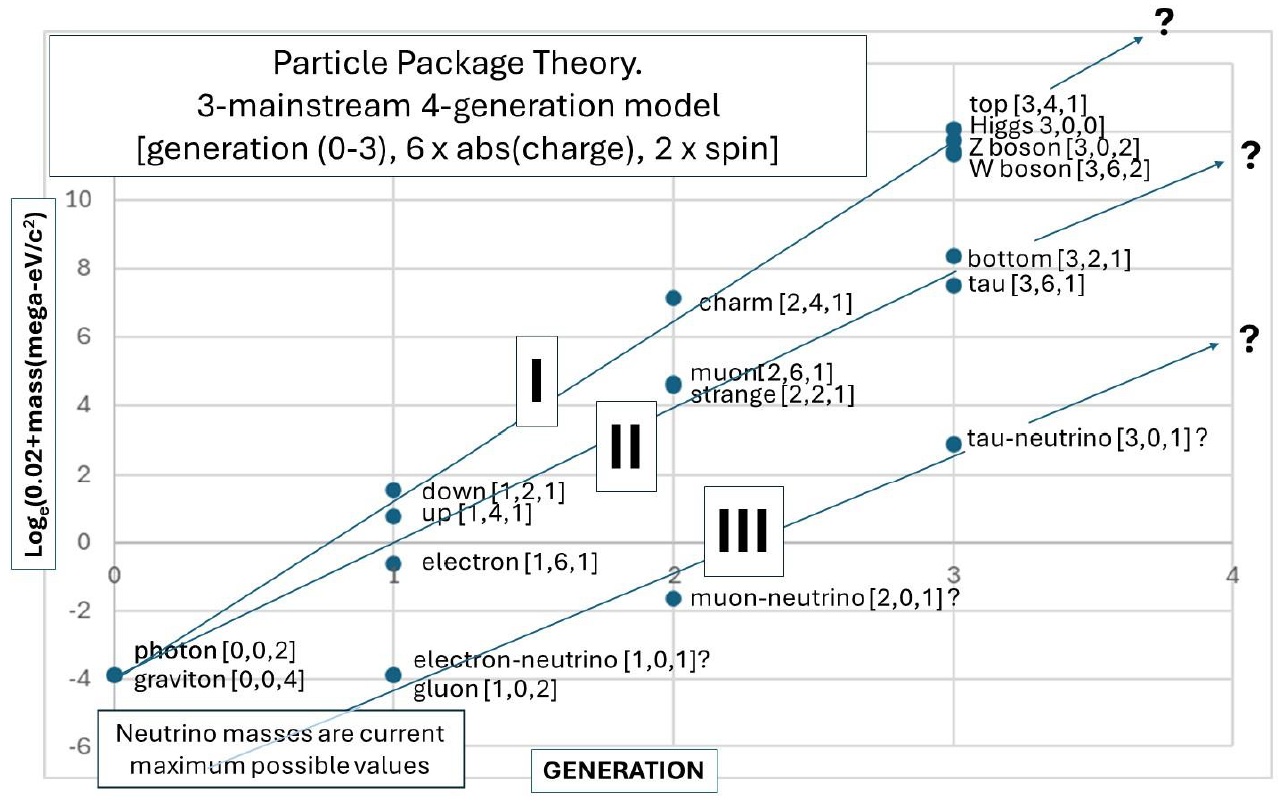
It is often stated that there is little obvious relationship between the rest mass energies in the standard model except that mass increases with generation in each one of the particle types, i.e. within the series of quarks, electron leptons and possibly neutrinos considered individually. However, this is misleading. Aclearer, more coherent, pattern emerges when (a) the notion of a generation number is treated as a quantum number divorced from separately considering each series, (b) when the particles are considered as arranged by the rest mass plus a small constant mass in the manner of a loop quantum field correction (with focus on the ”package” that somehow holds the particles of similar mass), and (c) when the logarithms of the mass-energies are plotted in a particular way against the generation number to include the photon, Higgs particle,Wand Z bosons, and a popular form of the conjectured graviton. The fact that the convenient use of log MeV/c2 mass energy is not
dimensionless is discussed. Three mainstreams I, II, III emerge from the clusters; the first two differ in slope and extrapolate to converge persuasively at a generation zero that is tempting to associate with massless spin 0 bosons, notably the photon, generating 11 clusters of mass energies with reasonably tight dispersion. It is suggested that the 4 generations may arise through a phase shift of π/2 related to 4 orthogonal superpositions of spins or bits |0>and |1>comprehensible in terms of axis rotations corresponding to progressive multiplication of the superpositions by imaginary number i. A projected mass energy for mainstream III, primarily the neutrino series, projected to generation zero, lies in the mass domain of axion-like particles (ALPs), still considered good dark matter candidates. The amplitude is more problematic, but, Chester’s pedagogical bead-on-a-circular- wire model provides a plausible explanation in terms of wavenumbers and kinetic energy as mass energy.