Four Cubes: On the Necessity of Four-Dimensional Perception

Szymon Łukaszyk

doi:10.59973/ipil.242

Authors

Szymon Łukaszyk Łukaszyk Patent Attorneys, Głowackiego 8, 40-052 Katowice, Poland

DOI:

https://doi.org/10.59973/ipil.242

Keywords:

Boolean space, Spectral graph theory, Sparse distributed memory, Activation functions, Neural architectures, Geometric deep learning, Cotan Laplacian, Exotic R4, Vector equilibrium, Ramanujan graphs, Topological data analysis, Emergent dimensionality

Abstract

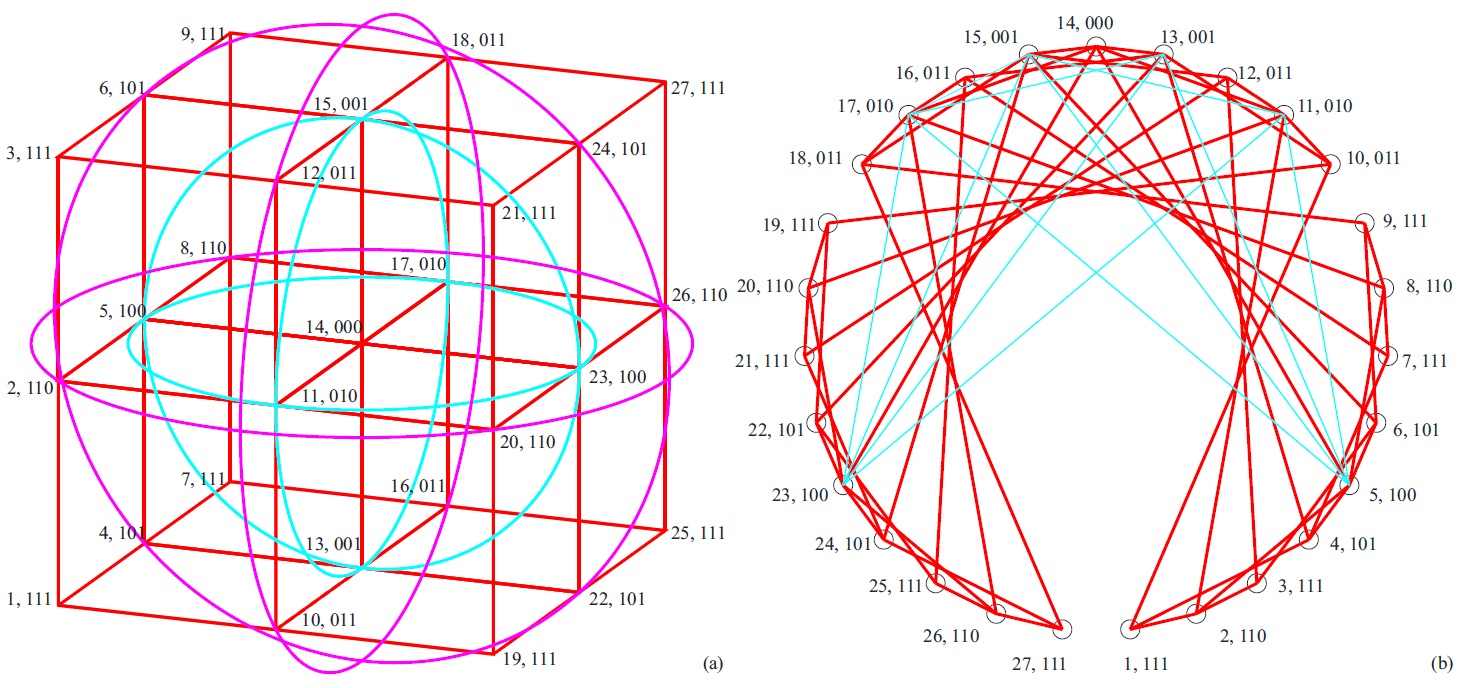
The study aimed to demonstrate that the perceived (3+0i)-dimensional space is necessary for biological evolution due to the exotic R⁴ property of such a space, which ensures variations of traits between individuals perceiving the same differentiable structures. Properties of graphs constructed in Boolean spaces {0, 1}ⁿ were researched. The cotan Laplacian of 2-face triangulated n-cube was shown to have a spectrum corresponding to the Hamming distance distribution of Boolean space, and its regular version was shown to be a Ramanujan graph for 2 ≤ n ≤ 5 with the smallest integral Ramanujan bound for n = 4. The spectrum of the distance matrix on the graph comprising 2ⁿ n-cubes sharing a common origin was shown to be bounded by irrational eigenvalues, and if its 2-faces are triangulated, the spectrum of the cotan Laplacian includes all integers from
0 to 3n without the eigenvalue of 3n − 1. The relations of these graphs with Buckminster Fuller’s vector equilibrium were discussed. Based on Watanabe’s ugly duckling theorem, we defined a trainable activation function of an artificial neuron in a sparse distributed memory model.

References

M. H. Poincar´e. Sur la dynamique de l’´electron. Rendiconti del Circolo matematico di Palermo, 21(1):129–175, December 1906. DOI: https://doi.org/10.1007/BF03013466

Karl Friston, James Kilner, and Lee Harrison. A free energy principle for the brain. Journal of Physiology-Paris, 100(1-3):70–87, July 2006. DOI: https://doi.org/10.1016/j.jphysparis.2006.10.001

Karl Friston. A free energy principle for a particular physics, 2019.

Ludwig Boltzmann. ¨Uber die Beziehung zwischen dem zweiten Hauptsatze der mechanischen W¨armetheorie und der Wahrscheinlichkeitsrechnung resp. den S¨atzen ¨uber das W¨armegleichgewicht [On the relationship between the second main theorem of mechanical heat theory and the probability calculation with respect to the results about the heat equilibrium], volume 2 of Cambridge Library Collection - Physical Sciences, page 164–223. Cambridge University Press, 2012. DOI: https://doi.org/10.1017/CBO9781139381437.011

Thomas S. Kuhn. Black-body theory and the quantum discontinuity: 1894-1912. Clarendon Press [u.a.], Oxford, 1978.

A N Kolmogorov. Combinatorial foundations of information theory and the calculus of probabilities. Russian Mathematical Surveys, 38(4):29–40, August 1983. DOI: https://doi.org/10.1070/RM1983v038n04ABEH004203

Mioara Mugur-Schachter. On a Crucial Problem in Probabilities and Solution, 2008.

David Jennings and Matthew Leifer. No return to classical reality. Contemporary Physics, 57(1):60–82, January 2016. DOI: https://doi.org/10.1080/00107514.2015.1063233

Michael Levin. Self-Improvising Memory: A Perspective on Memories as Agential, Dynamically Reinterpreting Cognitive Glue. Entropy, 26(6):481, May 2024. DOI: https://doi.org/10.3390/e26060481

Mathieu Desbrun, Eva Kanso, and Yiying Tong. Discrete differential forms for computational modeling. In ACM SIGGRAPH ASIA 2008 courses on - SIGGRAPH Asia ’08, pages 1–17, Singapore, 2008. ACM Press. DOI: https://doi.org/10.1145/1508044.1508059

Hirani, Anil Nirmal. Discrete exterior calculus. PhD thesis, California Institute of Technology, June 2003.

Szymon Łukaszyk and Andrzej Tomski. Omnidimensional Convex Polytopes. Symmetry, 15(3):755, March 2023. DOI: https://doi.org/10.3390/sym15030755

Andrei Markov. Regular Polytopes in Zn, 2011.

Pentti Kanerva. Sparse distributed memory. MIT Press, Cambridge, Mass, 1988.

Satosi Watanabe. Epistemological Relativity. Annals of the Japan Association for Philosophy of Science, 7(1):1–14, 1986. DOI: https://doi.org/10.4288/jafpos1956.7.1

S. Lukaszyk. A new concept of probability metric and its applications in approximation of scattered data sets. Computational Mechanics, 33(4):299–304, March 2004. DOI: https://doi.org/10.1007/s00466-003-0532-2

Satoshi Watanabe. Knowing and guessing: a quantitative study of inference and information. Wiley, New York, 1969.

Tomasz Szandała. Review and Comparison of Commonly Used Activation Functions for Deep Neural Networks. In Akash Kumar Bhoi, Pradeep Kumar Mallick, Chuan-Ming Liu, and Valentina E. Balas, editors, Bio-inspired Neurocomputing, volume 903, pages 203–224. Springer Singapore, Singapore, 2021. DOI: https://doi.org/10.1007/978-981-15-5495-7_11

Andrea Apicella, Francesco Donnarumma, Francesco Isgr `o, and Roberto Prevete. A survey on modern trainable activation functions. Neural Networks, 138:14–32, June 2021. DOI: https://doi.org/10.1016/j.neunet.2021.01.026

Krishnagopal Dharani. Dendrites and Primary Thoughts. In The Biology of Thought, pages 109–122. Elsevier, 2015. DOI: https://doi.org/10.1016/B978-0-12-800900-0.00006-3

Ilya Prigogine and Isabelle Stengers. Order out of Chaos: Man’s New Dialogue with Nature. Bantam Books, 1984.

Chris Fields, James F. Glazebrook, and Antonino Marcian `o. Reference Frame Induced Symmetry Breaking on Holographic Screens. Symmetry, 13(3):408, March 2021. DOI: https://doi.org/10.3390/sym13030408

Szymon Łukaszyk. Black Hole Horizons as Patternless Binary Messages and Markers of Dimensionality, chapter 15, pages 317–374. Nova Science Publishers, 2023.

G. ’t Hooft. Dimensional Reduction in Quantum Gravity, 1993.

Szymon Łukaszyk. Life as the explanation of the measurement problem. Journal of Physics: Conference Series, 2701 (1) : 012124 , Feb 2024. DOI: https://doi.org/10.1088/1742-6596/2701/1/012124

Crane, Keenan. The n-dimensional cotangent formula. https://www.cs.cmu.edu/˜kmcrane/

Projects/Other/nDCotanFormula.pdf, 2019. Accessed: 2025-07-13.

Max Wardetzky. A Primer on Laplacians. Taylor & Francis, CRC Press, Boca Raton, 2017.

Renjie Chen, Yin Xu, Craig Gotsman, and Ligang Liu. A spectral characterization of the Delaunay triangulation. Computer Aided Geometric Design, 27(4):295–300, May 2010. DOI: https://doi.org/10.1016/j.cagd.2010.02.002

Samuel Rippa. Minimal roughness property of the Delaunay triangulation. Computer Aided Geometric Design, 7(6):489–497, November 1990. DOI: https://doi.org/10.1016/0167-8396(90)90011-F

Charles L. Lawson. Transforming triangulations. Discrete Mathematics, 3(4):365–372, 1972. DOI: https://doi.org/10.1016/0012-365X(72)90093-3

A. Cantoni and P. Butler. Eigenvalues and eigenvectors of symmetric centrosymmetric matrices. Linear Algebra and its Applications, 13(3):275–288, 1976. DOI: https://doi.org/10.1016/0024-3795(76)90101-4

Klitzing. Re: what is the 5d vector equilibrium? http://hi.gher.space/forum/viewtopic.php?f=32&t=2207#p25149, 2016. Accessed: 2025-07-13.

Amy C. Edmondson. A Fuller Explanation. Birkh¨auser Boston, Boston, MA, 1987. DOI: https://doi.org/10.1007/978-1-4684-7485-5

Ricard Sol´e, Melanie Moses, and Stephanie Forrest. Liquid brains, solid brains. Philosophical Transactions of the Royal Society B: Biological Sciences, 374(1774):20190040, June 2019. DOI: https://doi.org/10.1098/rstb.2019.0040

Monica Gagliano, Michael Renton, Martial Depczynski, and Stefano Mancuso. Experience teaches plants to learn faster and forget slower in environments where it matters. Oecologia, 175(1):63–72, May 2014. DOI: https://doi.org/10.1007/s00442-013-2873-7

Clifford Henry Taubes. Gauge theory on asymptotically periodic {4}-manifolds. Journal of Differential Geometry, 25(3), January 1987. DOI: https://doi.org/10.4310/jdg/1214440981

Robion C. Kirby and L. Siebenmann. Foundational essays on topological manifolds, smoothings, and triangulations. Number no. 88 in Annals of mathematics studies. Princeton University Press, Princeton, N.J, 1977. DOI: https://doi.org/10.1515/9781400881505

Robert E. Gompf. Three exotic R4’s and other anomalies. Journal of Differential Geometry, 18(2), January 1983. DOI: https://doi.org/10.4310/jdg/1214437666

Donald D. Hoffman. Sensory Experiences as Cryptic Symbols of a Multimodal User Interface. Activitas Nervosa Superior, 52(3-4):95–104, September 2010. DOI: https://doi.org/10.1007/BF03379572

Johannes Jaeger, Anna Riedl, Alex Djedovic, John Vervaeke, and Denis Walsh. Naturalizing relevance realization: why agency and cognition are fundamentally not computational. Frontiers in Psychology, 15:1362658, June 2024. DOI: https://doi.org/10.3389/fpsyg.2024.1362658

Massimiliano Proietti, Alexander Pickston, Francesco Graffitti, Peter Barrow, Dmytro Kundys, Cyril Branciard, Martin Ringbauer, and Alessandro Fedrizzi. Experimental test of local observer independence. Science Advances, 5(9):eaaw9832, September 2019. DOI: https://doi.org/10.1126/sciadv.aaw9832

ˇCaslav Brukner. On the Quantum Measurement Problem. In Reinhold Bertlmann and Anton Zeilinger, editors, Quantum [Un]Speakables II, pages 95–117. Springer International Publishing, Cham, 2017. DOI: https://doi.org/10.1007/978-3-319-38987-5_5