On the "Assembly Theory and its Relationship with Computational Complexity"

Szymon Łukaszyk

doi:10.59973/ipil.157

Authors

Szymon Łukaszyk Łukaszyk Patent Attorneys, Głowackiego 8, 40-052 Katowice, Poland

DOI:

https://doi.org/10.59973/ipil.157

Keywords:

assembly theory, assembly index, information theory, Complexity classes, Mathematical physics

Abstract

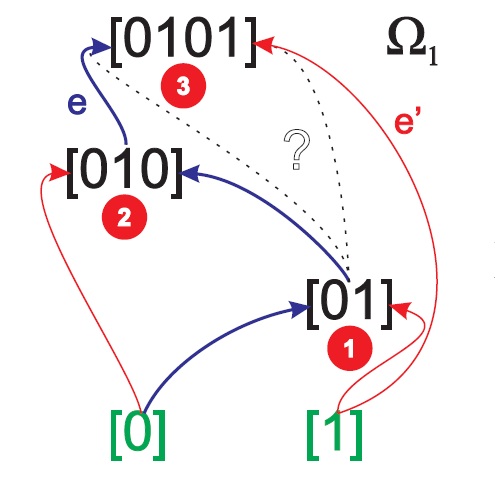
The study provides an alternative definition of the assembly space as an acyclic, 2-in-regular digraph of strings provided with an edge labeling map that preserves the commutativity of an assembly step but defines the order of concatenation of strings in this step. Remarkably, the uniqueness of each vertex is the sufficient criterion to establish if an assembly step is allowed and to introduce the notion of an assembly pool: unit-length strings cannot be assembled from shorter strings and, hence, are inaccessible, forming the initial assembly pool, and strings present in the assembly space can not be assembled again, possibly using different pathways, as they would not be unique. What is allowed is the evolution of assembly pathways to make them shorter. We also comment on certain results of [ARXIV.2406.12176], showing that the Assembly Steps Problem, not the Assembly Index Problem, has been proved in the referenced study to be NP-complete.

References

C. P. Kempes, M. Lachmann, A. Iannaccone, G. M. Fricke, M. R. Chowdhury, S. I. Walker, and L. Cronin, Assembly Theory and its Relationship with Computational Complexity, (2024). https://doi.org/10.48550/ARXIV.2406.12176

S. Łukaszyk, W. Bieniawski, Assembly Theory of Binary Messages, Mathematics, (2024). https://doi.org/10.3390/math12101600 DOI: https://doi.org/10.20944/preprints202401.1113.v10

W. Bieniawski, P. Masierak, A. Tomski, and S. Łukaszyk, Assembly Theory. Formalizing Assembly Spaces and Discovering Patterns and Bounds (2024). https://doi.org/10.20944/preprints202409.1581.v8

S.M. Marshall, A.R.G. Murray, L. Cronin, A Probabilistic Framework for Identifying Biosignatures Using Pathway Complexity,

Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 375, 20160342 (2017). https://doi.org/10.1098/rsta.2016.0342 DOI: https://doi.org/10.1098/rsta.2016.0342

S. Pagel, A. Sharma, L. Cronin, Mapping Evolution of Molecules Across Biochemistry with Assembly Theory, (2024). https://doi.org/10.48550/ARXIV.2409.05993

A. Sharma, D. Cz´egel, M. Lachmann, C.P. Kempes, S.I. Walker, L. Cronin, Assembly theory explains and quantifies selection and evolution, Nature, 622, 321-328 (2023). https://doi.org/10.1038/s41586-023-06600-9 DOI: https://doi.org/10.1038/s41586-023-06600-9